1.)†
![]() †can be expressed in
†can be expressed in
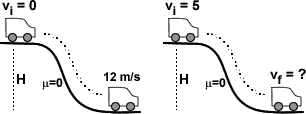
2.) A truck at rest at the top of the hill rolls down and achieves a speed of 12 m/s at the bottom. In a second experiment, the same truck has an intial speed of 5 m/s at the top of the hill. Its speed vf at the bottom will be:
 ††††
††††
3.)† It takes 10 Nm of work to compress an ideal spring 12 cm.† How much work does it take to†compress it 24 cm?
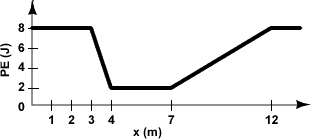
4.)† A 2.0 kg particle with total energy of 6 J is trapped in the potential "well" below.† When the particle is at† x = 3.5 m, its acceleration is: [hint: calculate the force and use Newton's 2nd law]
 †
†
†††††††††††††††††††††††††††††††††††
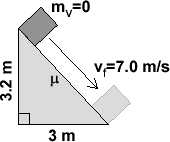
5.)†When the m = 2kg block slides down the plane,†it reaches a final speed at the bottom of vF = 7.0 m/s. The initial potential energy dissipated as heat is:
6.)† A tennis racket strikes a tennis ball with a force† F = F(t) whose graph is shown below:
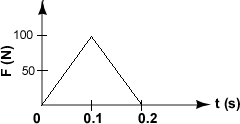
The total linear momentum change ∆p given to the tennis ball is:
7.) The center of mass of the two particles below is at x cm =
![]() †
†
8.)† Two identical hockey pucks collide on horizontal, frictionless ice.† ††††††††††††††††††††††††††††††††††††
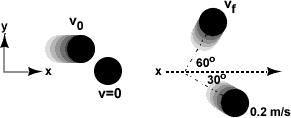
What must be the final speed vf of the top puck?
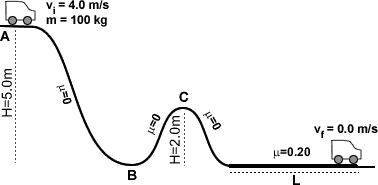
1.)†A small roller coaster of mass m has an initial horizontal speed of 4.0 m/s at point A at the top of the hills.† It rolls down over the smaller hill and coasts horizontally a distance L and comes to a stop. Calculate: [You must start with a physical law and then proceed logically, step-by-step, to obtain full credit.† Don't forget units in your answer.]
2.)† A bullet of mass m1 and horizontal speed vo strikes a stationary block of mass m2.†Calculate (in symbols):† [You must start with a physical law, write complete equations and include every step in your answer to get full credit.]††††††††
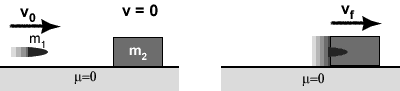
KE initial = total KE of system of m1 + m2 before bullet strikes m2
KE final = total KE of system of m1 + m2 after bullet comes to rest in m2.