|
Part I. ____ Part II. 1. ____ 2. ____ Total: ____ |
Part I. Do all 8 questions. 5 pts each
1.) The units of angular acceleration are:
2.) A thin metal hoop of mass M and radius R rolls without slipping with an
angular speed ![]() and
a center of mass speed vCoM. The total kinetic energy of the hoop is: (hint:
and
a center of mass speed vCoM. The total kinetic energy of the hoop is: (hint:
![]() = vCoM/R)
= vCoM/R)
3.)
The rotational inertia I of the system shown below is:
|
(massless rod) |
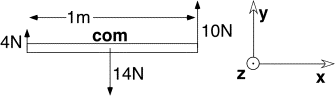
4.)
The total torque in Nm on the 1 m rod about an axis through the center
of mass is:
|
 |
5.)
A thin metal hoop and a solid cylinder have the same angular speed
![]() , the same mass
M, and the same radius R. The ratio of
the cylinder's kinetic energy to the hoop's kinetic energy is:
, the same mass
M, and the same radius R. The ratio of
the cylinder's kinetic energy to the hoop's kinetic energy is:
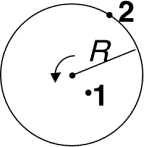
6.) A solid rigid cylinder of radius R
rotates with a constant angular speed
![]() about an axis through its center and out of
the paper. Point #1 is R/3 out from the
center and point #2 is on the rim.
about an axis through its center and out of
the paper. Point #1 is R/3 out from the
center and point #2 is on the rim.
The ratio (v2/v1) of the tangential speed v2 of point #2 to the tangential speed v1 of point #1 is:
|
 |
7.) Referring to the
cylinder of question 6 above, if
![]() is
increasing, both points #1 and #2 have the same:
is
increasing, both points #1 and #2 have the same:
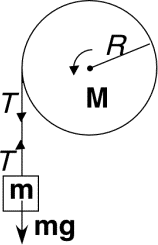
8.) The wheel of mass M and radius R is accelerating as shown because of the hanging mass m. The friction at the wheel's fixed axis of rotation is zero.
The torque acting on the wheel is:
|
 |
Part II. Do both problems. 30 pts each. Be neat. Write complete equations. You must show absolutely all your work to receive full credit.
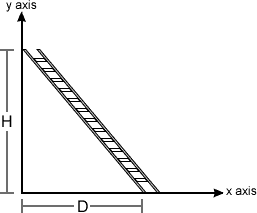
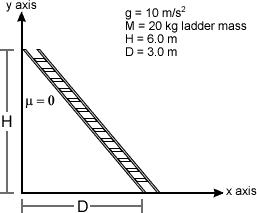 1.) A uniform ladder leans against a vertical frictionless wall. There is friction on the floor.
1.) A uniform ladder leans against a vertical frictionless wall. There is friction on the floor.
 2.) A uniform thin rod of
length L and mass M can rotate in a horizontal plane about a vertical axis
through its center. The rod is at rest
when a bullet of mass mB, traveling in the horizontal plane of the
rod, is fired into the end of the rod.
The bullet lodges in the rod and the rod and bullet then rotate
counterclockwise with an angular speed
2.) A uniform thin rod of
length L and mass M can rotate in a horizontal plane about a vertical axis
through its center. The rod is at rest
when a bullet of mass mB, traveling in the horizontal plane of the
rod, is fired into the end of the rod.
The bullet lodges in the rod and the rod and bullet then rotate
counterclockwise with an angular speed
![]() .
.